Elektrochemische Gassensoren
 Historische Darstellung zur Elektrochemie
Historische Darstellung zur Elektrochemie
Einführung
Elektrochemische Gassensoren nutzen die Freisetzung von Elektronen, die bei bestimmten chemischen Reaktionen entstehen können für eine gasanalytische Messung. Diese elektrochemischen Reaktionen beinhalten immer den Transfer von Ladungsträgern von einer Elektrode in eine andere Phase (Elektrolyt). Der Elektrolyt kann dabei sowohl fest, gelartig oder flüssig sein. Während dieses Prozesses finden an der Elektrode sowohl chemische Veränderungen als auch der Ladungstransport durch den Elektrolyten statt. Sowohl die Elektrodenreaktion als auch der Ladungstransport kann dabei chemisch beeinflusst werden. Sie ist Grundlage des Messvorganges. Zu den grundlegenden Regeln elektrochemischer Sensoren gehört, dass mindestens eine zweite Elektrode benötigt wird, um eine elektrochemische Zelle zu bilden. Die chemischen Reaktionen, die in einem elektrochemischen Sensor ablaufen, können sehr komplex sein. Im Folgenden werden daher nur die wesentlichen elektrochemischen Vorgänge und die messtechnischen Eigenschaften beschrieben.
Flüssigelektrolytsensoren
In Abb.1 ist der prinzipielle Aufbau eines elektrochemischen Gassensors mit einem Flüssigelektrolyten dargestellt. Da das Elektrolytmaterial flüssig ist, muss es sich in einem Behälter befinden, der nach allen Seiten verschlossen ist. Lediglich von einer Seite kann das Gas über eine durchlässige Membrane in das Innere des Gassensors gelangen. Diese Membrane verhindert gleichzeitig das Auslaufen der Elektrolytflüssigkeit. Auf der Rückseite der Membrane befindet sich die Messelektrode, in Form einer dünnen leitfähigen Platin- oder Gold-Schicht. Diese Elektrodenschicht ist ebenfalls für das Gas durchlässig. An der Messelektrode findet bereits die erste chemische Reaktion statt. Für einen CO-Sensor wäre das die folgende Reaktion:
(1) 2CO + 2H2O → 2CO2 + 4H+ + 4e-
Es entsteht an der Messelektrode also Kohlendioxid, das durch die Membrane wieder nach außen gelangt. Die H+-Ionen wandern dann zur Gegenelektrode, wo sie mit den an der Messelektrode frei gesetzten Elektroden zu Wasser rekombinieren. Die Elektroden gelangen über den äußeren Stromkreis zur Gegenelektrode und bilden somit den Messstrom IM. An der Gegenelektrode findet dann folgende Reaktion statt:
(2) 02 + 4H+ + 4e- → 2H2O
Die Gesamtreaktion ergibt sich aus den beiden Teilreaktionen wie folgt:
(3) 2CO + O2 → CO2
Der für die Gesamtreaktion erforderliche Sauerstoff kommt aus der Umgebungsluft und gelangt ebenfalls über die Membrane in den Reaktionsbereich. Für jedes CO-Molekül, das über die Membrane in den Sensor gelangt, entstehen demnach 2 Elektronen (→ z=2), die im Messstrom IM erfasst werden. Aus diesem einfachen Zusammenhang erkennt man sofort, dass die Kennlinie eines elektrochemischen Gassensors mit einem Flüssigelektrolyten ein lineares Verhalten aufweist. In der Regel wird der Messstrom über einen Lastwiderstand geleitet und man misst dann den Spannungsabfall über diesem Widerstand RL. Die Messspannung UM ergibt sich dann aus:
(4) UM = IM · RL
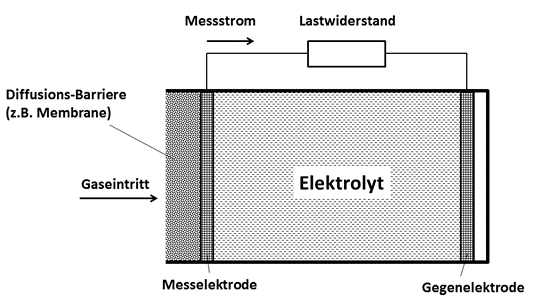 Abb.1: Prinzipieller Aufbau eines elektrochemischen Gassensors nach dem amperometrischen Verfahren.
Abb.1: Prinzipieller Aufbau eines elektrochemischen Gassensors nach dem amperometrischen Verfahren.
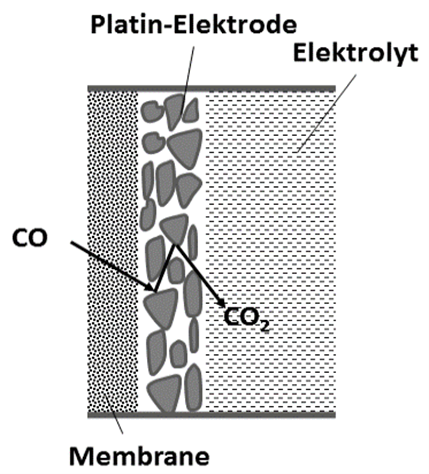 Abb. 2: Teilansicht der Platinelektrode als poröse Schicht auf der gasdurchlässigen PTFE-Membrane. Die erste Teilreaktion findet also bereits in der dünnen Pt-Schicht statt.
Abb. 2: Teilansicht der Platinelektrode als poröse Schicht auf der gasdurchlässigen PTFE-Membrane. Die erste Teilreaktion findet also bereits in der dünnen Pt-Schicht statt.
Nach dem 1. Faraday´schen Gesetz lässt sich dann aus den voran gegangenen Überlegungen den Messstrom IM berechnen:
(5) IM = z · F · Q
Der Faktor F ist die Faraday1 -Konstante mit F=NL·e=96486,7 As/mol und Q=dN/dt der Stoffumsatz in mol/s. Die Anzahl der Elektronen, die pro Gasmolekül freigesetzt werden, wird mit z bezeichnet. Daraus ergibt sich für IM:
(6) IM = z · F ·
Wird der Transport der Teilchen hauptsächlich durch Diffusion vorgegeben, so erhält man mit dem 1. Fick´schen Gesetz für IM folgenden Ausdruck:
(7) IM = z · F · D · A ·
Der Messstrom IM ist demnach proportional zur Eintrittsfläche A in den Gassensor und proportional zu dem temperaturabhängigen Diffusionskoeffizienten D(T). Δc ist die Differenz der Teilchendichte (Konzentration) über der Diffusionsschicht Δx. Da die Teilchendichte an der Messelektrode gleich Null ist, steigt der Messstrom auch proportional zu c an. In Abb.3 ist die typische Kennlinie eines elektrochemischen Gassensors dargestellt. Aufgrund von unvermeidbaren Leckströmen ist der Messstrom bei c=0 von Null verschieden. Diesen Wert bezeichnet man als Nullpunktstrom (Zero-Current). In dem angeführten Beispiel (CO-Sensor) beträgt dieser Nullpunktstrom max. 150 nA. Die Empfindlichkeit S liegt für diesen Gassensor bei S = 30nA/ppm +/- 12nA/ppm. Die Toleranzbreite ist groß, aber durchaus typisch für diese Art von Gassensoren und muss daher im Gasmessgerät berücksichtigt werden.
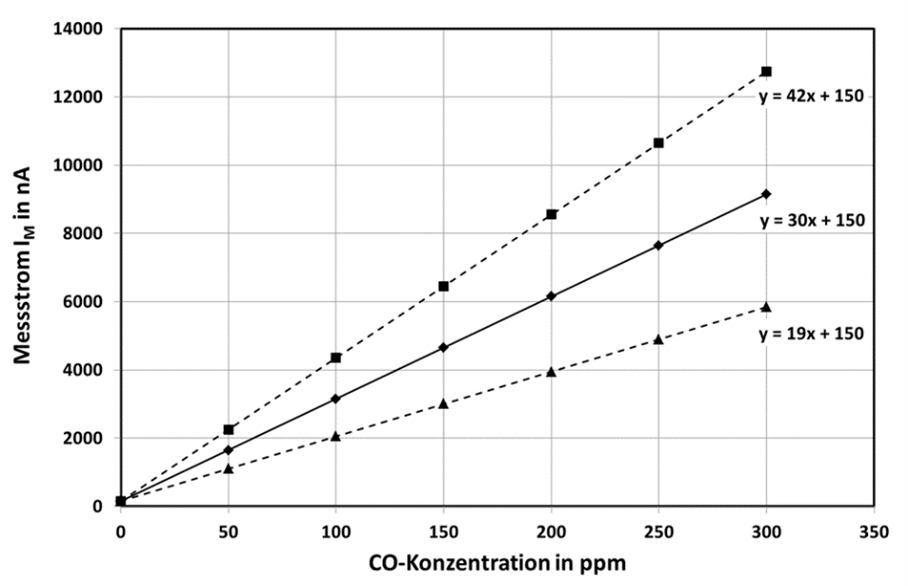 Abb. 3: Kennlinie eines elektrochemischen CO-Gassensors. Die durchgezogene Linie zeigt den typischen Kennlinienverlauf, während die gestrichelten Linien den maximal zulässigen Toleranzbereich angeben.
Abb. 3: Kennlinie eines elektrochemischen CO-Gassensors. Die durchgezogene Linie zeigt den typischen Kennlinienverlauf, während die gestrichelten Linien den maximal zulässigen Toleranzbereich angeben.
Elektrochemischer Sauerstoffsensor
Eine Besonderheit unter den elektrochemischen Gassensoren ist der Sauerstoffsensor. Er basiert auf den gleichen physikalischen und chemischen Gesetzmäßigkeiten, die bereits beschrieben wurden. Er ist allerdings für hohe O2-Konzentrationen ausgelegt, die bis 100 Vol.-% reichen. In den meisten technischen Anwendungen (z.B. Verbrennungsvorgänge) wird eine Sauerstoffkonzentration im Bereich von 0 bis 21 Vol.-% erwartet. Der Maximalwert entspricht dem Sauerstoffgehalt in der Umgebungsluft. Durch den Verbrennungsvorgang wird ein Teil des Sauerstoffs umgewandelt und somit reduziert sich dieser Anteil entsprechend. Über den Sauerstoffgehalt können also Rückschlüsse auf den Verbrennungsprozess gezogen werden. Ähnlich sieht es bei medizinischen Anwendungen aus, wenn es um eine Atemgasanalyse geht. Auch in diesen Fällen liegen Sauerstoffkonzentration im Vol.-% Bereich vor.
In Abb.4 ist ein solcher Sauerstoffsensor dargestellt. In dem dichten Sensorgehäuse (Kunststoff) befindet sich ein flüssiger Elektrolyt (z.B. verdünnte Essigsäure). In dem Elektrolyten ist eine massive Metallanode eingebracht, während die Kathode sich als dünne Goldschicht auf der gasdurchlässigen Membrane befindet. Der empfindlichen Membrane ist noch zusätzlicher mechanischer Schutz (Blende) vorgeschaltet, durch das Gas aber problemlos diffundieren kann.
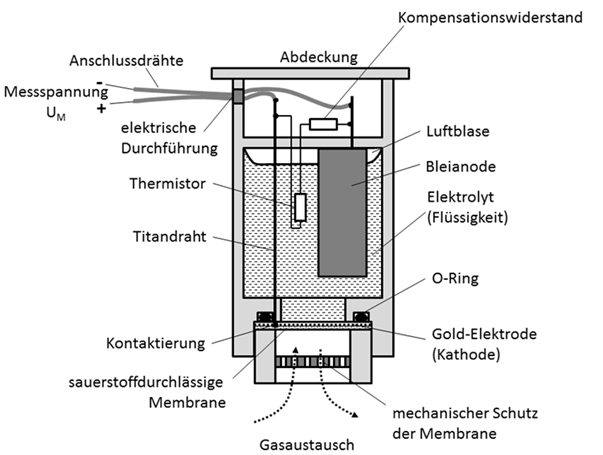 Abb. 4: Querschnitt durch einen elektrochemischen Sauerstoffsensor mit einem Flüssigelektrolyten
Abb. 4: Querschnitt durch einen elektrochemischen Sauerstoffsensor mit einem Flüssigelektrolyten
An den Elektroden finden folgende Reaktionen statt:
(8) Kathoden - Raktion: O2 + 4H+ + 4e- → 2H2O
(9) Anoden - Raktion: 2PB + 2H2O → 2PbO + 4H+ + 4e-
(10) gesamte Raktion: O2 + 2Pb → 2PbO
Pro Sauerstoffmolekül entstehen demnach 4 Elektronen (→z=4). Wichtig ist auch die Gesamtreaktion. Sie zeigt uns, dass der Sauerstoff im Sensor mit dem Blei der Anode zu Bleioxid oxidiert. Die Sauerstoffmoleküle, die zum Messeffekt beitragen, „verbrauchen“ quasi die Anode im Laufe der Messzeit kontinuierlich. Die Lebensdauer dieser Sensorvariante hängt also direkt von der zu messenden O2- Konzentration ab. Die Lebensdauerangabe erfolgt bei diesem Sensor daher in %-O2 x Stunden. Typische Werte liegen bei 0,5·106 Vol.%·h. Ein Sensor, der permanent in atmosphärischem Sauerstoff (≈21 Vol.-%) arbeitet, lebt demnach ca. 3 Jahre. Sind die mittleren Sauerstoffkonzentrationen geringer, lebt der Sensor entsprechend länger. Die Betriebstemperatur hat einen zusätzlichen Einfluss auf die Lebensdauer.
Der Kennlinienverlauf ist auch in diesem Fall linear und ebenfalls mit einer großen Bandbreite (+/- 25%) hinsichtlich der Empfindlichkeit behaftet. In Abb.5 ist die Bandbreite der Kennlinien zu sehen. In der Auswerteelektronik (Basisboard) wird diese Bandbreite durch eine einfache Endpunktjustage mit Umgebungsluft auf 21 Vol.-% kalibriert.
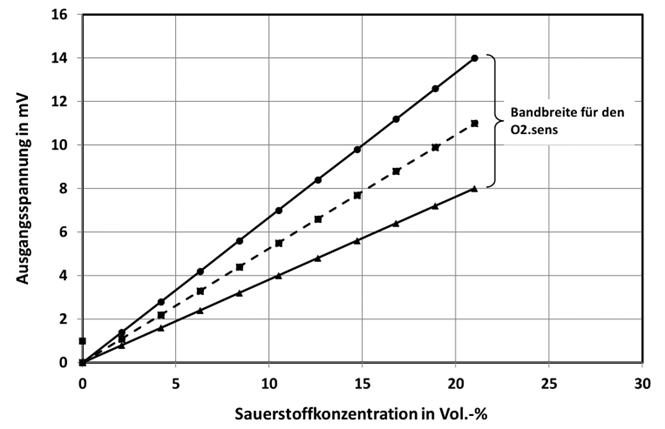 Abb. 5: Bandbreite der Kennlinien des O2.sens im nicht kalibriertem Zustand
Abb. 5: Bandbreite der Kennlinien des O2.sens im nicht kalibriertem Zustand
In Abb. 6 ist der Gassprung von 100% Stickstoff auf ≈21 Vol.-% Sauerstoff (Luft) für unterschiedliche Sauerstoffsensoren zu sehen. Der O2.sens hat mit einer dünnen Membrane ein deutlich schnelleres Ansprechverhalten, da die Diffusion besser ist als bei einer dicken Membrane.
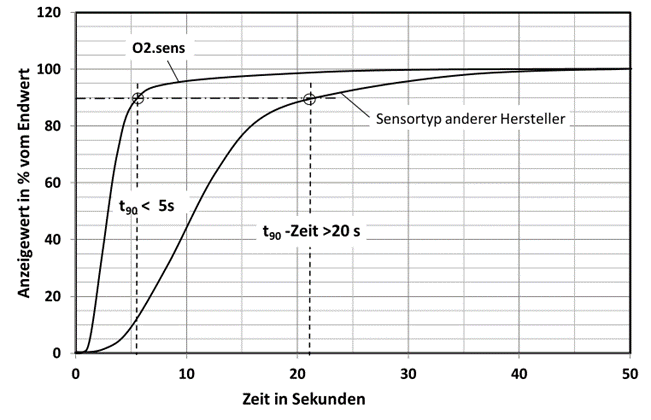 Abb.6: Zeitliches Ansprechverhalten für zwei unterschiedliche Sensorversionen
Abb.6: Zeitliches Ansprechverhalten für zwei unterschiedliche Sensorversionen
Druckabhängigkeit
Der Messstrom hängt linear mit der Teilchendichte n vor der Membrane zusammen. Wird die Teilchendichte z.B. durch eine Druckänderung erhöht, steigt der Messstrom linear an. Es gilt dann folgender Zusammenhang:
(11) IM(p) = IM(1013hPa) ·
In Abb.7 ist der Verlauf der Messspannung in Abhängigkeit vom Luftdruck pL dargestellt. Typischerweise wird ein maximaler Druckbereich von pL =800 bis1200 hPa spezifiziert.
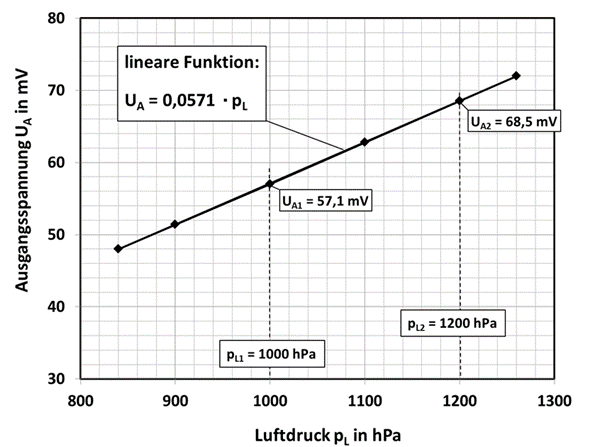 Abb. 7: Abhängigkeit der Messspannung vom Luftdruck bei einer Sauerstoffkonzentration von ≈21 Vol.-%.
Abb. 7: Abhängigkeit der Messspannung vom Luftdruck bei einer Sauerstoffkonzentration von ≈21 Vol.-%.
Temperaturkompensation
Da die Diffusionsrate der Sauerstoffmoleküle durch die Membrane mit der Temperatur ansteigt, ändert sich auch der Messstrom entsprechend. Für genaue Messungen muss dieser Temperaturfehler kompensiert werden. Die einfachste Möglichkeit besteht darin, als Lastwiderstand eine Kombination aus Festwiderständen und temperaturabhängigen Widerständen einzusetzen. Im einfachsten Fall kann eine Reihenschaltung aus einem Festwiderstand R1 und einem Thermistor R2 genutzt werden (Abb.10). Der Widerstandswert des Thermistors hat ein NTC2 -Verhalten und nimmt mit der Temperatur ab, so dass der Spannungsabfall UM bei konstantem Messstrom IM ebenfalls abnimmt. Steigt der Messstrom, infolge einer Temperaturerhöhung, so bleibt der Spannungsabfall konstant und das Messsignal ist temperaturkompensiert. Dazu muss allerdings das Verhältnis zwischen R1 und R2 so gewählt werden, das diese Kompensation vollständig ist. Wird R1 >> R2 so ist der gesamte Lastwiderstand nahezu unabhängig von der Temperatur. Wird R2 >> R1 so ist der Durchgriff wesentlich größer. Das Temperaturverhalten eines Thermistors lässt sich wie folgt beschreiben:
(12) R2(T) = R25 · eB·( - )
Die Messspannung UM ergibt sich dann aus:
(13) UM = IM(T) · [R1 + R25 · eB·( - )]
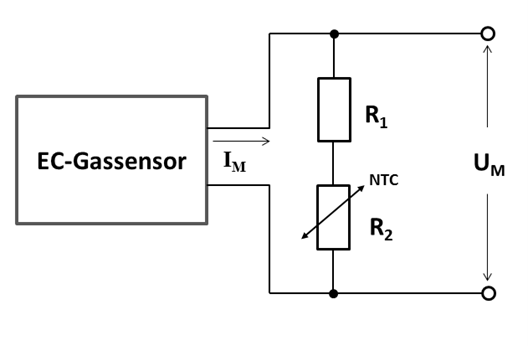 Abb.8: Externe Beschaltung eines elektrochemischen Gassensors zur Temperaturkompensation mit einem Thermistor (NTC).
Abb.8: Externe Beschaltung eines elektrochemischen Gassensors zur Temperaturkompensation mit einem Thermistor (NTC).
In Abb.9 ist der Messstrom in Abhängigkeit der Temperatur dargestellt. IM(T) steigt mit der Temperatur an, während der Widerstand Rges. mit der Temperatur abfällt. Durch R1 kann dieses gegenläufige Verhalten angepasst werden, damit der Messstrom dann unabhängig von der Temperatur wird. Das Ergebnis dieser Anpassung ist in Abb.10 zu sehen. Eine nahezu vollständige Kompensation wird im Temperaturbereich von 15-35°C erreicht. Bei höheren oder auch tieferen Temperaturen steigt der Fehler dann an. Da sich der Thermistor in der Elektrolytflüssigkeit befindet dauert es natürlich eine gewisse Zeit bis sich die Temperaturen angepasst haben. Für schnelle Temperaturänderungen kann der Thermistor auch außerhalb des Sensors platziert werden, um die Reaktionszeit zu reduzieren.
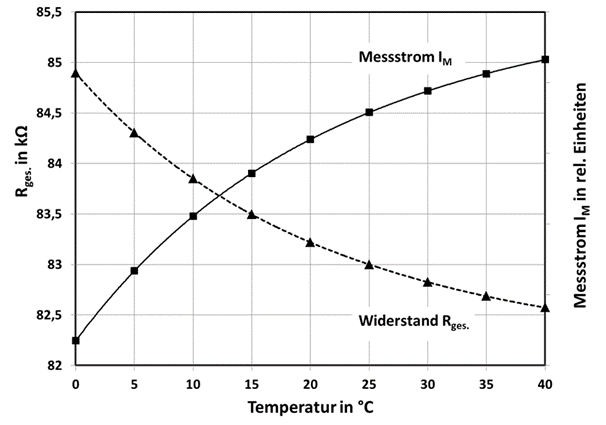 Abb. 9: Temperaturverhalten des Gesamtwiderstandes Rges. und des Messstromes IM.
Abb. 9: Temperaturverhalten des Gesamtwiderstandes Rges. und des Messstromes IM.
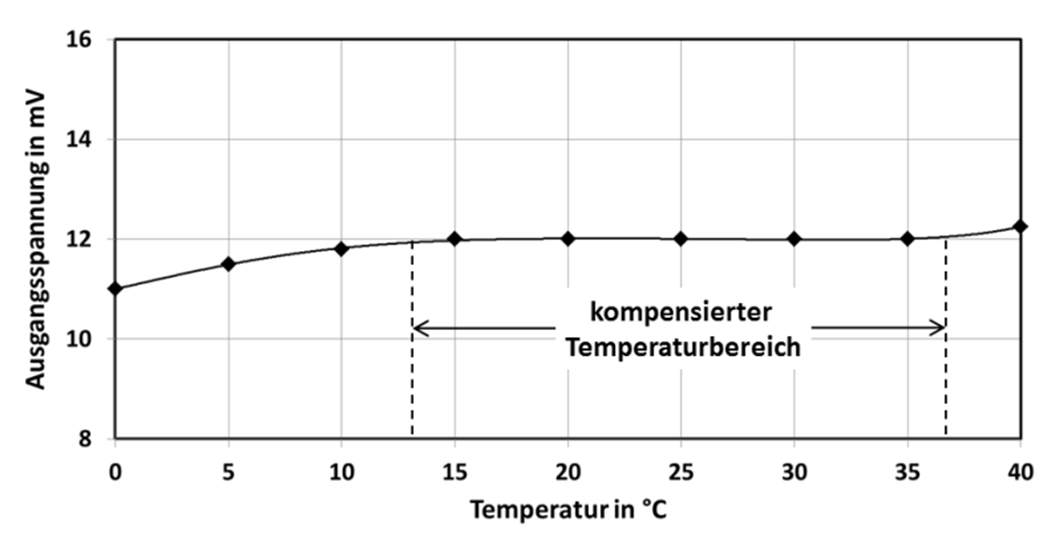 Abb.10: Kompensierte Ausgangsspannung UM im Temperaturbereich von 0°C bis 40°C.
Abb.10: Kompensierte Ausgangsspannung UM im Temperaturbereich von 0°C bis 40°C.
Driftverhalten
Die irreversible Veränderung der maximalen Messspannung wird als Drift bezeichnet. Dazu wird der Sensor mit einer konstanten Gaskonzentration (z.B. ≈21 Vol.-% O2) über einen langen Zeitraum (mehrere Monate) beströmt. Die Signalveränderungen sind bei den einzelnen Sensoren individuell verschieden. In Abb.11 ist das Driftverhalten über einen Zeitraum von 12 Monaten angegeben. Der O2.sens würde demnach anstatt der vorgegebenen 21 Vol.-%O2 nur noch 18,9 Vol.-% O2 anzeigen. Wird eine höhere Genauigkeit gefordert, so muss Monate nachjustiert werden. Bei einer monatlichen Justage würde sich die Anzeige maximal von 21 Vol.-% O2 auf 20,83 Vol.-% O2 ändern.
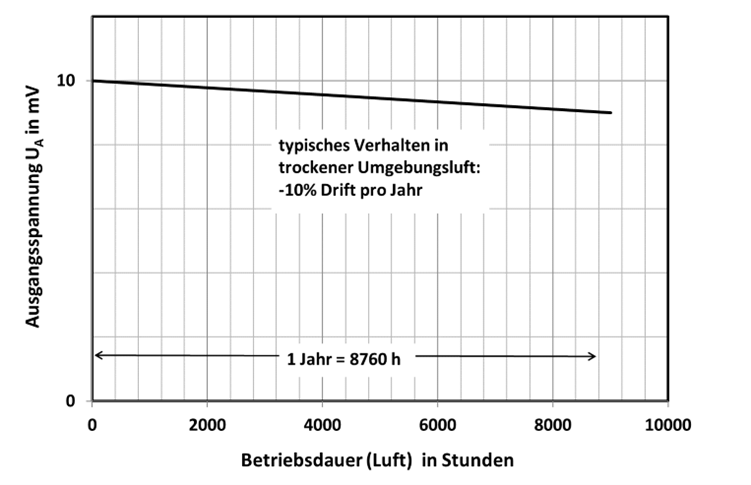 Abb.11: Driftverhalten elektrochemischer Gassensoren in Luft mit einem Sauerstoffgehalt von ≈21 Vol.-% O2.
Abb.11: Driftverhalten elektrochemischer Gassensoren in Luft mit einem Sauerstoffgehalt von ≈21 Vol.-% O2.
 Abb. 12: O2.sensD mit digitaler Schnittsteller zur störungsfreien Übertragung der Sensordaten zur Auswerteelektronik (Mainboard)
Abb. 12: O2.sensD mit digitaler Schnittsteller zur störungsfreien Übertragung der Sensordaten zur Auswerteelektronik (Mainboard)
1 Michael Faraday (1791-1867) englischer Naturforscher und bedeutender Experimentalphysiker
2 Negativ Temperature Coefficent














